騒音の発生機構と発生音のスペクトル
流体内に圧力変動が生じると、その圧力変動が周囲に伝わり音になります。ここでは、この圧力変動の発生機構と、それによって生じる騒音のスペクトルを対応付けて解説します。これらのことを利用すれば、騒音源や異音源の特定に役立ちます。
単一ピークのスペクトル
スペクトルに1つの鋭いピーク、またはなだらかなピークを生じる音源としては以下のものがあります。
1)部材の共振
機械は稼働時に必ず振動を発生します。例えば、ギアなどの部品で一旦振動が発生すると接触している周囲へ振動が伝わり、薄板のような剛性の小さい部材に振動が伝わればその部材が大きく振動し、大きな騒音を発生します(強制振動)。特に、その部材の固有振動数と発生した振動の振動数が近いと剛性の小さい部材が大きく振れ、結果として大きな騒音が発生します。このとき騒音のスペクトルには鋭いピークが生じます。
具体例として以下のものがあります。
① 圧縮機につながる配管系があり、その先に大きなボックスがある場合に、圧縮機の振動がボックスにまで伝わり、ボックスが共振する。
② ギアボックスにギアの振動が伝わり、ギアボックスが共振する。
③ 軸受箱に軸受の振動が伝わり軸受箱が共振する。
2)回転軸の共振
回転軸が危険速度に近い回転数で回転している場合、回転軸は大きき振動し、回転軸につながる部位を大きく揺らします。これにより大きな騒音が発生し、騒音のスペクトルには鋭いピークが発生します。
3)空力音
流体が流れると流体内に乱れが生じ、音が発生します(流体音、空力音)。流れによって生じる音の中には比較的滑らかなスペクトルになる騒音と鋭いピークが生じる騒音があります。
滑らかなスペクトルになるものとして以下のものがあります。このスペクトルは特定の周波数でピークを持ちますが、周辺と比較して際立ったピークになることはありません。
① 噴流音
吹き出し口から噴流が出るときに、騒音が発生します。これは、噴流と周囲の静止流体の相互作用で流体に乱れが生じるためです。流体と流体の相互作用で騒音が発生する場合は、騒音の強度は流速の8乗に比例します(Lighthillの8乗則)。この時のスペクトルは比較的平坦なものになりますが、以下の周波数f(Hz)になだらかなピークが生じます。
ここで、St:ストローハル数(無次元)、u:流速(m/s)、D:出口の代表寸法(m)です。円形ダクトの場合の代表寸法はダクトの内径です。なお、亜音速域ではストローハル数は通常0.2~0.3程度になります。
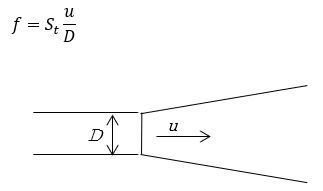
図1 噴流音
② グリル騒音
冷暖房機の吹き出し口などで、流れにより整流用のグリルから騒音が発生します。この騒音は流れと物体の相互作用で発生する乱れにより発生します。発生する騒音強度は流速の4乗に比例します。この時のスペクトルは比較的平坦なものになりますが、以下の周波数f(Hz)になだらかなピークが生じます。
ここで、St:ストローハル数(無次元)、u:流速(m/s)、D:グリル開口の代表寸法(m)です。
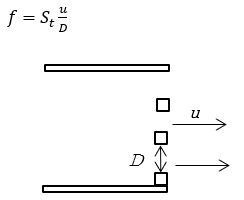
図2 グリル騒音
一方、以下のカルマン渦による騒音のスペクトルは鋭いピークを持ちます。
③ カルマン渦
流体の流れの中に円柱などの構造物があると後流に交互に渦が発生します。この渦はカルマン渦と呼ばれており、騒音が問題になる場合や構造物が振動して破壊に至ることもある現象です。また、ボイラなどで熱交換器の管群の後流に空洞などがある場合、空洞の共鳴を起こす可能性があります。これは流れの後流に生じる渦によって構造物が振動することで発生します。電線が風に吹かれて音を出すことがありますが、これと同じ機構で音が発生ます。これらは構造物の自励振動によるもので、流速などが特定の条件の時に発生します。
このとき、スペクトルに以下の周波数f(Hz)に鋭いピークが生じます。
ここで、St:ストローハル数(無次元)、u:流速(m/s)、D:構造物の代表寸法(m)です。
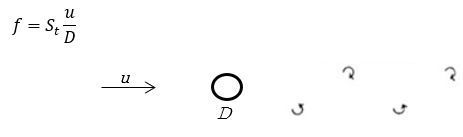
図3 カルマン渦
等間隔ピーク群
定期的にほぼ同じパターンの騒音が発生すると、そのスペクトルには等間隔のピークが生じます。繰返しの周期をT秒とすると、1/T Hzの周波数とその整数倍の周波数にピークが生じます(高調波)。なお、発音原理は違いますが、楽器の音も基本周波数成分とその高調波成分で構成されます。
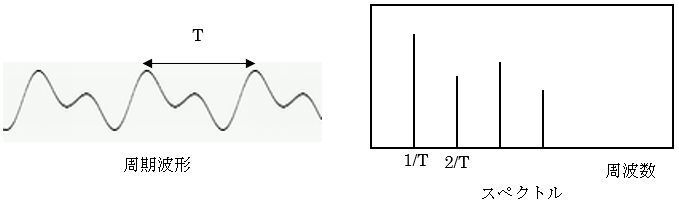
図4 周期波形とそのスペクトル
機械の部品として以下のものが使用されている場合はよく発生する騒音です。
1)ギア
2)玉軸受
3)回転翼
ギアの場合は駆動側が1枚の歯で荷重を支える時間帯と2枚の歯が荷重を支える時間帯があり、このため歯元の応力が繰り返し変動します。
玉軸受の場合は、軸の角度によって1つの球で荷重を受け持つときと2つの球で荷重を受け持つ時間帯があり、このことで部品に定期的な応力変動が生じます。
回転翼の場合は、翼の後流で乱れが定期的に生じるために騒音が発生します。
これらの騒音の基本周波数は以下により計算可能です。
ギ ア:回転数(rpm)÷60×歯数 (噛み合い周波数)
玉軸受:回転数(rpm)÷60×球数
回転翼:回転数(rpm)÷60×翼数
4)スティックスリップ
比較的よく発生するものとして、スティックスリップ現象があります。これは接触した固体同士が特定の範囲の接触圧力かつ相対速度を持つときに発生する音で、自励振動の範疇に入ります。
黒板をチョークでなぞったときの音、自転車のブレーキ音、ドアの開閉時に発生する音などがあります。珍しい例としてはサイロに貯蔵された小さなプラスチック片をサイロの下から取り出すときに、特定の条件でトラックの警笛音或いは像の鳴き声のような音が発生することがありますが、これもスティックスリップ音です。
5)共鳴
同様なスペクトルを持つものとして、配管内の流体などの共鳴現象があります。配管では何らかの原因で乱れが発生すると、配管の端部でその乱れが反射し発生源のところに戻りますが、その時に反射波が発生源のところと同相になる周波数では乱れが増大するため、大きな音が発生します(固有振動数)。固有振動数は、配管の長さと音速で計算することができます。
笛などの楽器の音がこれに当たります。また、往復動圧縮機により流体を吐出する配管系においては、配管の固有振動数において大きな変動圧が発生します。ただし、スティックスリップ音が比較的よく発生することと比較すると、機械でこのような現象が発生することは多くありません。ボイラでカルマン渦により共鳴が起こることなどが知られています。
6)打撃音
部品が定期的に打撃されるときに発生する騒音のスペクトルは共鳴と同様なものになります。打撃音と共鳴音はスペクトルでは違いが出ないときがありますが、スペクトログラムでは違いを出せます。共鳴音の場合は連続音のため固有振動数成分の音の強度は変化しません。一方、打撃音の場合は打撃が生じたときに大きなレベルになり、そうでないときは小さなレベルになります。
制御弁のポペットが自励振動を起こし弁座に定期的に衝突する場合にこのような現象が生じます。
7)キャビティ音
流体の流れの中に窪みがあると窪みで共鳴が生じ、スペクトルには以下の周波数f(Hz)に鋭いピークが生じます。更に、高調波も励起される場合があります。
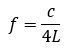
ここで、 c:音速(m/s)、L:窪みの深さ(m)です。
図のように、窪みの先端で乱れが生じ、その乱れが窪みの深さ方向の共鳴を起こします。
万年筆の蓋に横から息を吹きかけると発生する音がこれに当たります。
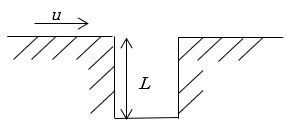
図5 キャビティ音発生機構
実際の機械音では多くの部品から生じる複数の系列のスペクトルの合成になり、複雑なスペクトルになります。また、上記に加えてなだらかなスペクトルを持つ燃焼音などもあります。この複雑なスペクトルから対策すべき部品を特定するのは容易ではありません。
当社では、長年の騒音対策経験を基に騒音対策を効率的に行うことができる、騒音対策に特化した信号処理ソフト「騒音分析ツール」を販売しています。従来の信号処理ソフトではデータ分析はできるものの、分析結果を騒音対策に活用することが難しい側面がありましたが、「騒音分析ツール」を使用すれば、騒音対策を効果的に支援する分析が可能です。
また、長年重工メーカーで騒音対策を行って来ましたので、waveファイルをお送り頂けば騒音分析を行い騒音源の特定や騒音対策案の策定などを行います。ビデオカメラの出力ファイルでも対応可能です。料金は10万円からです。お気軽にお問い合わせください。
