異音検査装置
StaVaTesterIW(スタバテスタ・アイ・ダブリュー)は、加振された部品の振動のスペクトル、または稼働中の機械から生じる音や振動のスペクトルを統計解析し、その特徴を基にパターン認識技術を適用して製品の良否検査を自動的に行う装置です。ものづくり現場での傷などの目視検査や耳による検査を自動化することができます。
異音検査装置
一般に、機械などから発生する音や振動などの特徴は、そのスペクトルやスペクトログラム(声紋)などに明瞭に現れることが知られており、検査ワークのスペクトルを良品のスペクトルと比較すれば、検査ワークの良否が簡単にわかります。しかし、スペクトルは周波数成分の数が数百から数千になるため、従来は、このような大量の特徴量を基に自動的に検査ワークの良否を判断する方法はありませんでした。
そこで、StaVaTesterIWは、スペクトルの標準化変量を基にする新しい類似度計算方法により、このような大量の特徴量を直接比較することを可能にしました(標準化変量と類似度は以後ご説明します)。このため、機械の音や振動の微妙な違いを検出することが可能になり、検査ワークの良否を精度よく自動検査することが可能になりました。なお、自動異音検査装置と銘打っていても人間による検査が不可欠なものも見られますが、StaVaTesterは無人自動検査を可能にします。
これによって、エンジンなどの良否の検査や内部欠陥の検査、プレス品の割れ検査などに適用できます。
StaVaTesterIWで使用しているパターン認識技術を使用する検査と振動によって傷の有無が分かる理由は以下に説明しています。
なお、この技術はこれまで行ってきた以下の検査技術を基礎として高度化したものです。
異音検査装置StaVaTesterIWの導入効果
StaVaTesterIWを導入することにより、以下の効果が得られます。
1)高速な異音検査・異常振動検査が可能です(検査時間数秒)。
2)高精度な異音検査・異常振動検査が可能です。統計解析により良品範囲を定義します。
3)客観的な検査データが得られます。波形とそのFFT(フーリエ変換)スペクトルを保存することができます。
4)安定した検査が可能です。
5)検査に熟練を必要としません。
6)製造工程の評価が可能です。
StaVaTesterIWは検査結果として類似度を出力します。類似度が1に近ければ品質が良いこと示すため、類似度の逐次推移や日平均推移・週平均推移・月平均推移を観察することで製造工程の健全度をチェックすることができます(オプション)。
また、類似度を大きな値に保持するように製造パラメータを調整することで、検査装置というよりも品質保証装置としても使用でき、良質な商品を生産することにつながります。
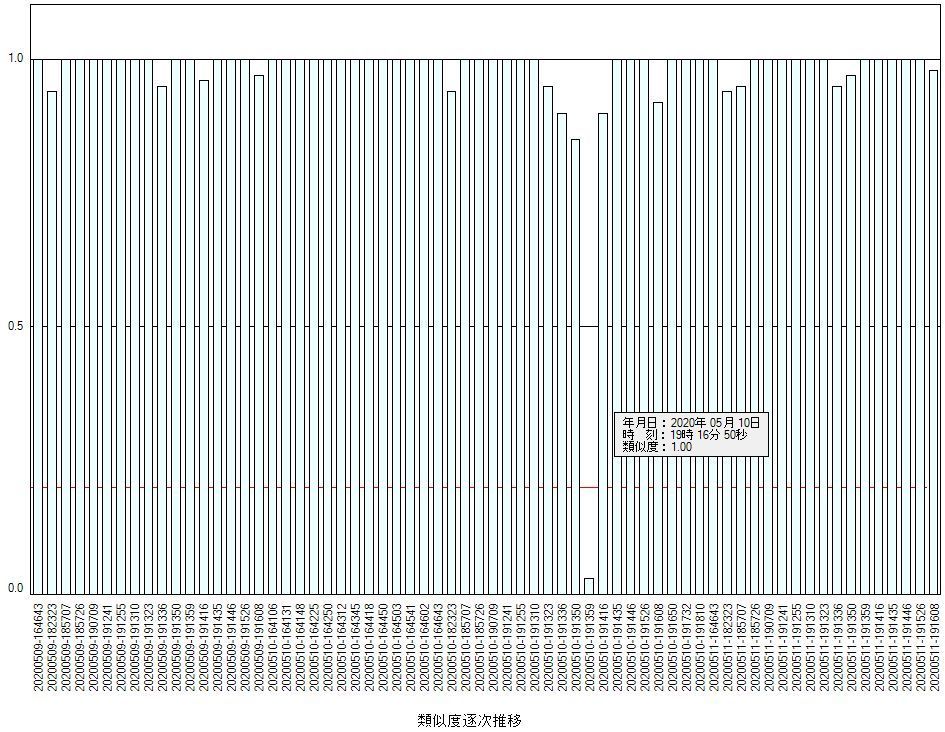
なお、科学的な検査を行うことで聴覚による検査では検出できなかった欠陥を検出した例が複数あります。これによって、製品の品質の向上につながっています。このように異音検査は科学的な方法が優位なため、異音検査の自動化により品質の向上と生産コストの低減を図ることをお勧めします。
異音検査装置StaVaTesterIWの適用分野
StaVaTesterIWは次の検査・診断に使用できます。
Ⅰ 製品検査
1)プレス品の割れや減肉などの検査
2)薄肉シリンダーの目視検査の自動化
3)深絞り品の目視検査の自動化
4)内部欠陥の検査
5)自動車エンジンやギア、モーターなどの機械製品の検査
6)パソコンやハードディスクなどの電気製品の検査
7)その他、音や振動の特徴を基に良否を判定することができる検査
Ⅱ 設備診断
1)設備機械の状態診断
2)その他、音や振動の特徴を基に良否を診断することができる状態診断
異音検査装置StaVaTesterIWの特長
StaVaTesterIWは次の特長を持っています。
1)品質評価が可能です。
検査ワークの品質を0から1の間の実数値で評価します。値が大きいほど品質が高い
ことを示します。
2)検査精度が高い。
検査ワークの音や振動のスペクトル強度の標準化変量を基に検査するため、高い検査
精度があります。
3)検査レシピが簡単に作成できます。
データ収集とFFT(高速フーリエ変換)の初歩的な知識しか必要としません。
4)検査レシピが素早く作成できます。

欠陥パネル
異音検査装置StaVaTesterIWの適用例
機械部品の傷検査の例を示します。右図のステンレス板の傷の有無によるスペクトルの違いを基に傷の有無を検査する例です。
板を加振し、その振動を計測します。計測結果のスペクトルを下図右に示します。上の図は振動波形です。青く示した部分のスペクトルを下の部分に示しています。赤い線は良品の平均スペクトルです。黒い線は検査ワークのスペクトルです。両者類似していますが、違いが見られます。この違いが大きいと傷の有無の検査ができます。なお、下の方に示した青い線は両者の差をデシベル表示したものです。広い周波数範囲にわたって違いが見られます。
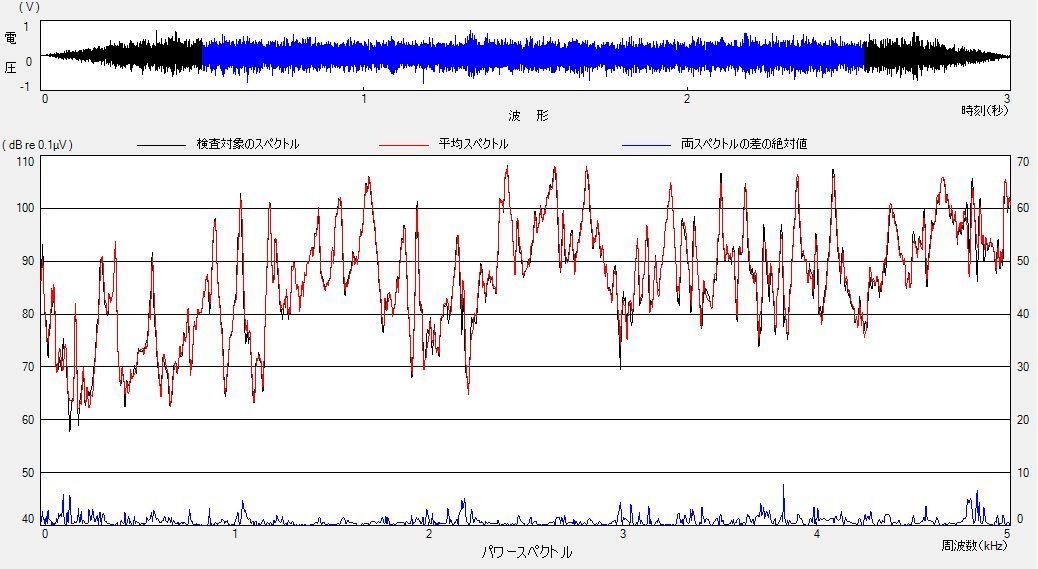
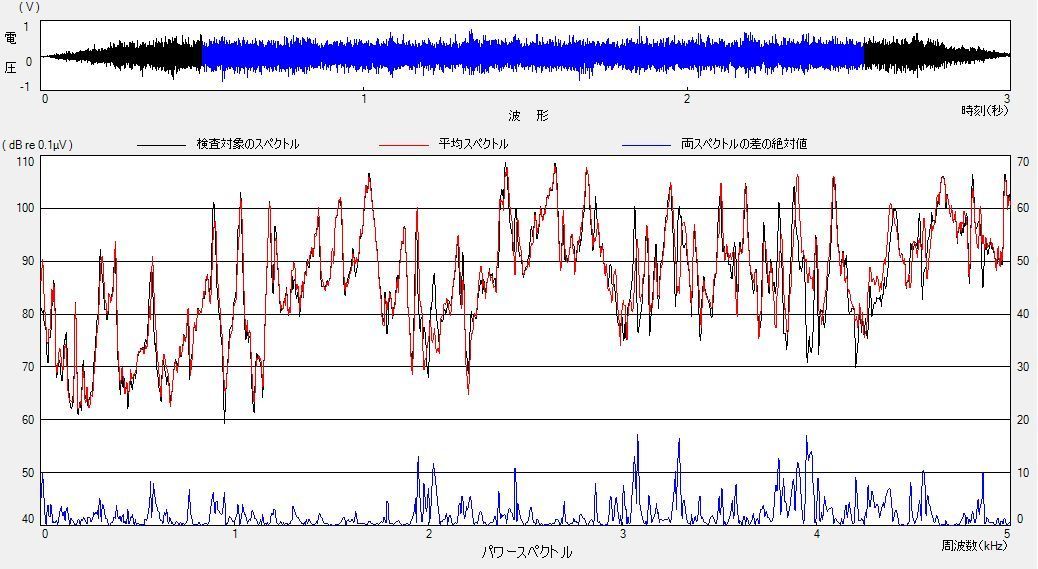
これまで、自動車のドアの割れ検出やアルミ製シリンダの表面及び内部欠陥、セラミックス製品の内部欠陥、深絞り品の内部欠陥などの振動特性を分析しています。また、検査ワークに応じた各種の加振方法と計測方法を適切に選択することや、振動の基礎知識と上記欠陥検査を通して得た豊富なノウハウを保有しています。
異音検査装置StaVaTesterIW製品ラインアップ
1)受動型(StaVaTesterIWP)
製品の稼働音・振動を計測し、そのスペクトルを基に製品の良否を検査する装置です。エンジン、ギア、モーター、パソコン、ハードディスクドライブなどの検査に使用できます。
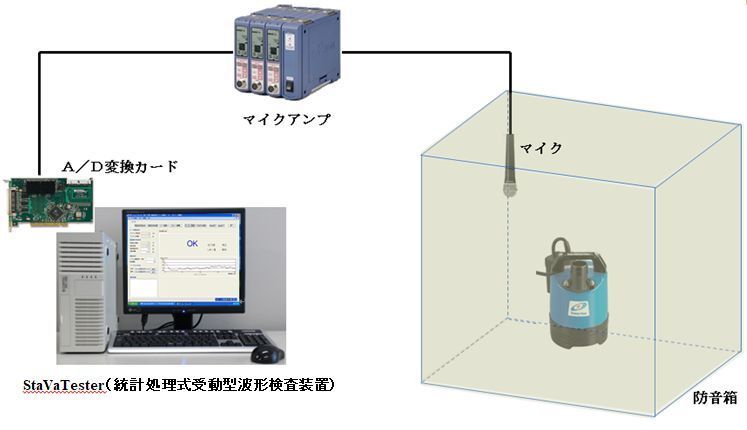
受動型StaVaTesterIW概念図
2)能動型(StaVaTesterIWA)
機械部品などを加振し、その時の部品の振動スペクトルを基に部品の良否を検査する装置です。
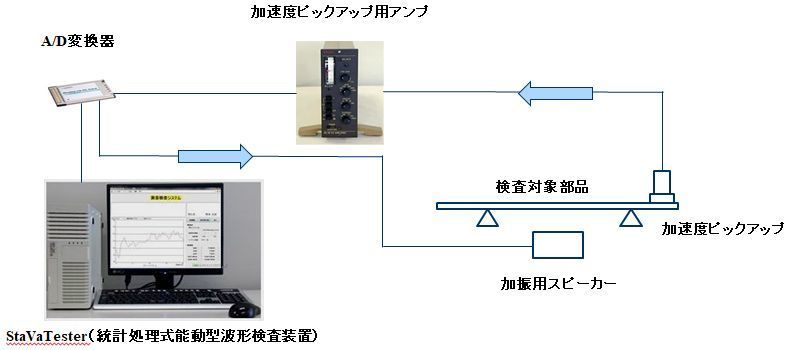
能動型StaVaTesterIW概念図
3)設備監視(StaVaTesterMW)
機器の発生する振動や音のスペクトルを監視して機器の状態を監視します。機械設備や工作機の状態を監視します。
異音検査装置StaVaTesterIWの仕様
StaVaTesterIWの基本仕様は以下の通りです。
検査時間
数秒 (計測+分析+判定:分析と判定には時間はほとんどどかかりません)
検査レシピ作成時間
数分から数十分程度 (除くデータ収集)
周波数範囲
0.1~100kHz (周波数範囲は使用するセンサに依存します)
アナライザ
ウィンドウズパソコン
異音検査装置StaVaTesterIWの検査フロー
StaVaTesterIWでは、異音検査・異常振動検査を通常のパターン検査と同様次のように行います。
1)マイクや振動センサを使用して検査ワークの音や振動を計測します。
2)FFT(高速フーリエ変換)により、波形のスペクトルを計算し、周波数毎に標準化変量(後述)を計算します。
3)波形の標準化変量を基に類似度計算(後述)を行い、その値がしきい値以上のときにOK、未満のときにNGと診断します。
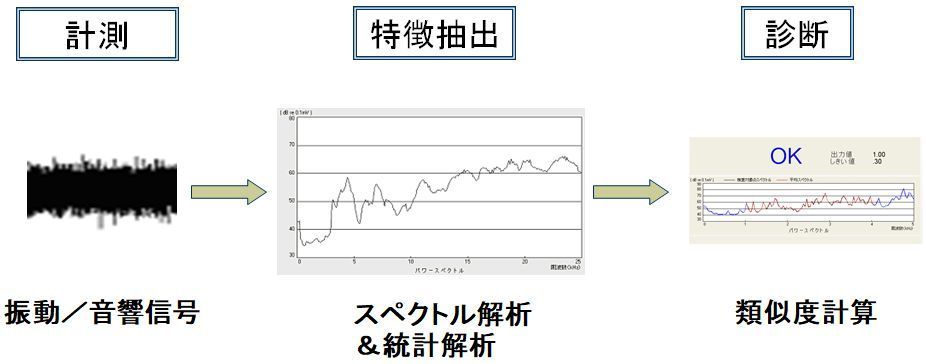
異音検査装置StaVaTesterIWの検査原理 - 標準化変量
StaVaTesterIWで使用する標準化変量は、検査ワークのスペクトル強度と良品の平均スペクトル強度の差を良品のスペクトル強度の標準偏差で割った値と定義されます。
標準化変量という用語はなじみの薄い統計量ですが、実際には検査でよく使われています。例えば、このワークの重さは良品の重さの平均±3σの間に入っているから良品と判断するといった検査がよく行われています。この時の±3が標準化変量です。そこで、スペクトルでも同様に、ある周波数の標準化変量値が小さいか大きいかでその周波数成分の良否が判断できます。
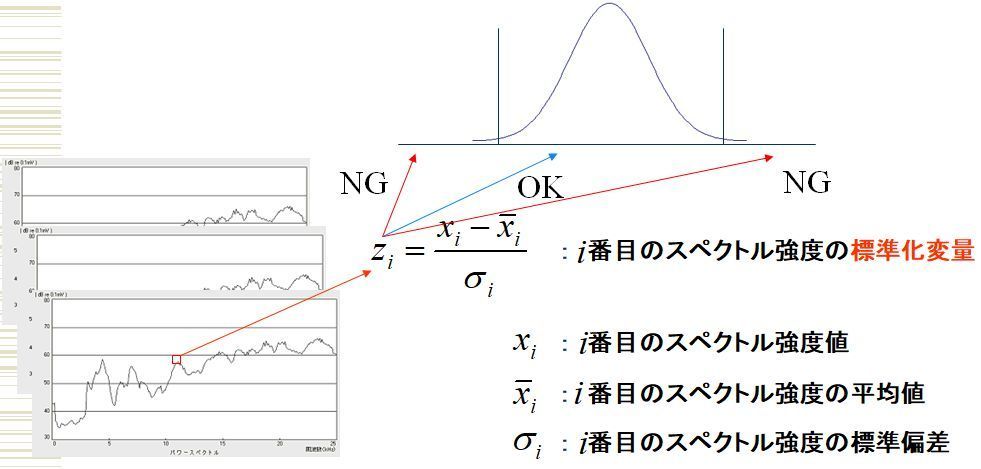
標準化変量の優位性を具体例で示します。下図の左の黒い線は良品のスペクトルを示しています。赤い線は良品の平均スペクトルを示しています。図の下の線は上記両スペクトルの差の絶対値を示しています。下図の右は不良品に対するものです。スペクトルの比較だけでは明瞭に良否を決めることはできません。
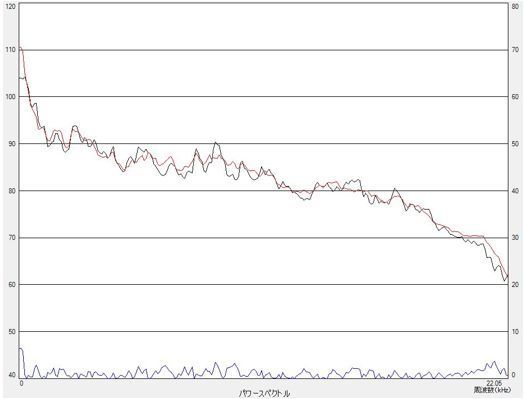
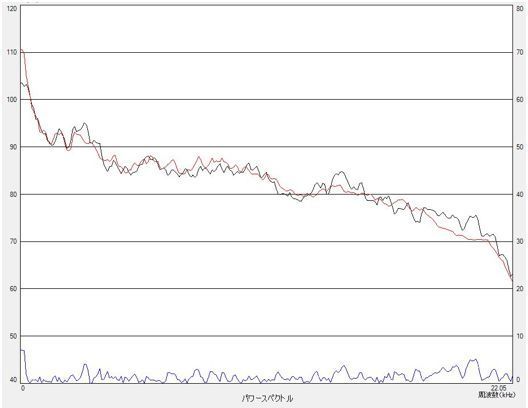
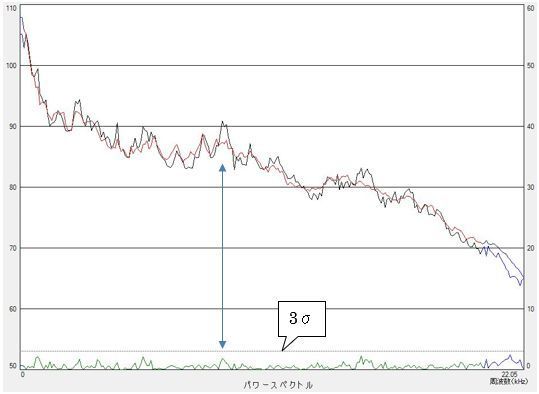
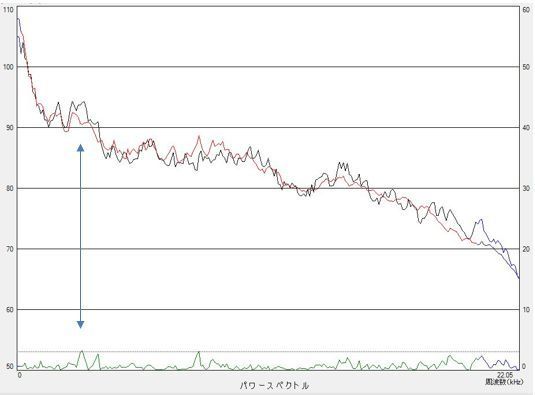
一方、下図の左は差の絶対値の代わりに標準化変量を示したものです。全体的に良品では3σに近い周波数成分はありませんが、不良品では3σに近い周波数成分が多数あります。また、矢印で示してい周波数では、平均スペクトルの差は良否であまり違いがありませんが、標準化変量では差が出ています。つまり、差が同じであってもその周波数における良品のスペクトルのばらつきが大きければ良品に近く、良品のスペクトルのばらつきが小さければ良品とは距離があることを示しています。
このように、標準化変量で表すと良否がわかりやすくなります。また、次項で説明している類似度を計算すると、良品では 1.0 不良品では 0.3 となり、良否判定が可能です。
以上のように、工業製品にはばらつきがあるため統計的な処理を施すことが重要です。
異音検査装置StaVaTesterIWの検査原理 - 類似度
スペクトルでは多数の標準化変量があるため、標準化変量によって周波数ごとの良否が分かっても、検査ワークの良否を判断することはできません。そこで、全周波数の標準化変量を総合して品質を定量化します。これまでは総合判断が不可能なため、標準化変量を使用する自動化装置が実現できませんでした。
StaVaTesterIWでは、新しい類似度計算式を使用することによりワークの良否を判断できるようになりました。

異音検査装置StaVaTesterIWの使用手順
StaVaTesterの使用手順は以下のようになります。
1)データ収集と検査可否の検討
2)検査レシピ作成と性能検討
3)検査
1)データ収集と検査可否の検討では、マイクや加速度ピックアップなどを使用してStavatesterのデータ収集機能により検査対象の音や振動の波形を収集します。サンプリング周波数と計測時間などを指定すれば簡単に行えます。次に、収集した波形のスペクトルを計算し、良品と不良品で違いがあるかどうかを確認します。これもStaVaTesterの機能を使用すると多数のスペクトルが簡単に比較できるため、良否による違いが簡単に確認できます。
2)検査レシピ作成と性能検討では、良品データの指定や検査周波数範囲、検査時間帯などを設定し、パラメータ調整ボタンをクリックすると、数秒から1分程度で検査レシピが作成されます。検査レシピが作成されたら、別の波形で検査性能を調査し、検査レシピが実際に使用できるかどうかを検討します。
3)検査では、作成した検査レシピを使用して検査ボタンをクリックすると検査が実行され、検査結果が表示されます。
以上のように、StaVaTesterを使用すれば短時間に簡単に検査レシピを作成することができます。

異音検査装置StaVaTesterIWの検査の種類
異音検査装置の検査の種類は以下の通りです。
1) 良否検査
良否を判定できる検査レシピを使用して、検査品が良品か不良品かを判定します。
2) 不良種類検査
良否を判定できる検査レシピと検査種類ごとの判定レシピを作成し、検査品の良否と不良の種類を検査します。
① 良否検査用レシピを使用して検査を行います。
② OK判定であればOK品とします。
NG判定であれば、順次不良種ごとの検査レシピを適用し、不良の種類を判定します。
NG品の種別を特定できるため、生産管理データとして使用できます。ギヤユニットで故障種別が判断できることが確認されています。
異音検査装置StaVaTesterIWの導入手順
異音検査装置の導入手順は以下の通りです。
①検査可能性の検討
御社製品の自動検査が可能かどうかを簡単に検討します。
検査対象機器の良品データ15~30と不良品データを対象として検討します。検査対象機器の音又は振動を計測頂きデータをお送り頂くか、検査対象機器をお送り頂ければ当方にて検査可能性について検討し、その結果を報告致します。
②実用性の検討
①の検討の結果、実用できる可能性がある場合、実際に使用できるかどうかを検討します。このため、多数のデータを対象に検査可能性を検討します。
弊社デモ機をお貸出し致しますので、お客様にて実用性を検討して頂きます。必要であれば、ご支援致します。デモ機お貸出し期間は2週間程度です。
③実機導入
実用性があると判断できる場合は、実機を製作致します。
- 主力商品・サービス
- お役立ち情報
- よくあるご質問
